
Bu yazı “Matematik Tarihindeki Bazı Krizler” adlı daha genişçe bir yazının ilk bölümü olarak okuyucuya sunulmaktadır.
Şirince’deki Nesin Matematik Köyü’nde bir seminer verirken matematikte antik çağlardan bu yana ortaya çıkmış krizlerden söz etmiştim. Bu yazıda matematik tarihinde meydana gelmiş devrimsel nitelikteki bazı krizleri kısaca anlatmak istiyorum.
Matematik tarihindeki ilk ve belki de en büyük krizlerden biri Antik Yunan’da Pisagor döneminde ortaya çıkmıştır. O dönemlerde Antik Yunan’da bir rasyonalizm geleneğinin olduğu bilinir. Varlığın mahiyetinin, maddenin, kesin bilginin ne olduğunu bilmek için öncelikle aklın bilgisini kullanmamız gerektiği, özellikle Sokratik dönemde ve sonrasında savunulan bir görüş olmuştur. Rasyonalizm, Platon’un Diyaloglar’ında sıkça üzerinde durulan ve Antik Yunan’da yöntem olarak benimsenmiş bir felsefi görüştür. Rasyonalizm, kesin bilginin sadece akıl yoluyla elde edildiğini savunan görüştür. Rasyonalizme karşılık deneycilik fikri ise, kesin bilginin sadece deneysel gözlem yoluyla elde edildiğini savunur. Düşünce tarihi boyunca çatışan bu iki fikirden rasyonalizm, Antik Yunan’da, özellikle Sokratik dönemde ön planda olan bir görüş olmuştur.
Sokratik öncesi dönemde Pisagor ve takipçilerinden oluşan Pisagorcular, evrende bir düzen olduğunu, bu düzenin doğal sayılarla ve doğal sayıların birbirlerine oranlarıyla açıklanabileceğini düşünmüşlerdir. Bu görüşe göre evren, ya da kosmos, doğal sayıların kuralları çerçevesinde anlaşılır bir şekilde çalışmaktadır. Pisagorculara göre evrendeki düzen, doğal sayıların bir dansıdır. Doğal sayılar ve doğal sayıların birbirleriyle oranlarının akılsal bir yönü vardır. Buna uymayan varlıklar anlaşılmazdır, kaotiktir.
√2 nin bulunuşu
Pisagorculuk felsefesinin sonunu yine Pisagorcular getirmiştir. Pisagor Teoremi’ni çoğu kişi lise geometri derslerinden bilir. Geometri’nin en temel teoremlerinden biri olan Pisagor Teoremi, bir dik üçgenin hipotenüsün uzunluğunun karesinin diğer iki kenarların uzunluğunun karelerinin toplamına eşit olduğunu söyler. Aşağıdaki şekilde verildiği gibi hipotenüse c, diğer iki kenara a ve b dersek, Pisagor teoremi bize olduğunu söylemektedir.
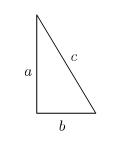
Şimdi, a=b=1 olarak alındığı zaman, yani birim kenar uzunluğunda bir dik üçgen alındığında, hipotenüsün uzunluğunun √2 olduğu görülür ki bu uzunluğun herhangi iki doğal sayının oranı ile ifade edilmesi mümkün değildir. √2 kesirli bir sayı değildir, yani günümüz matematik terminolojisiyle rasyonel sayı değildir.√2 irrasyonel bir sayıdır. Rasyonel kelimesi Latin kökenli bir sözcüktür, ratio kökünden gelir. Ratio’nun kelime anlamı kesir ya da oran olmasına rağmen rational yani rasyonal kelimesi akılsal demektir. İngilizce’de rational kelimesinin anlam olarak kökeni Antik Yunanca’da “konuşma”, “konuşulan” anlamına gelen logos sözcüğünden gelir. Nitekim, Antik Yunan’da hipotenüsün bu uzunluğuna alogos denmiştir. Alogos, Antik Yunanca’da “(hakkında) konuşulamayan” demektir. Pisagorculara göre doğal sayıların veya onların oranlarıyla açıklanamayan şeylerin bilgisi hakkında konuşulamadığından dolayı, bu sayıya alogos denmiş. √2 bugünün terminolojisiyle bir reel sayıdır, 1.41421356… şeklinde giden sonsuz basamaklı bir ondalık sayı olarak kabul edilir.
Sonsuz küçüklükler ve kalkülüs
√2 sayısının bulunuşuyla beraber matematikte artık kesirli olmayan sayılar kabul edilmiştir. √2’nin bulunuşu, sonsuz olan ile sonlu olan arasındaki ayrımı daha da netleştirmiştir. Kesirli sayıların gösterimi m/n şeklinde sonlu bir gösterimdir. √2 hiçbir şekilde doğal sayıları kullanarak sonlu bir gösterime sahip olamaz. Sonlu ile sonsuz arasındaki bu ayrım, yüzyıllar sonra, 17’nci yüzyılda Isaac Newton ve Gottfried W. Leibniz’in bağımsız çalışmaları sonucunda sonsuzluk kavramının matematiğe dahil edilmesiyle ortaya tekrar çıkmıştır. Bugün kalkülüs (calculus) olarak bilinen ve matematiğin en temel dallarından biri haline gelen bu alan, aslında fiziğin de problemlerini idealize bir zeminde çözmek için geliştirilmiş ve fiziksel olguları matematiksel olarak modellemek için bulunmuş, devrim niteliğinde bir alandır. Kalkülüs, sürekli (continuous) bir zemindeki değişim matematiği olarak görülebilir. Bir aracın t ile t+n zaman aralığındaki ortalama hızını kolayca hesaplayabiliriz. t ile t+n arasındaki zaman ‘sürekli’ olarak kısaldıkça, fark tam 0 olduğunda, belli bir t anındaki ortalama hızı bulmak cebirsel yöntemlerin dışına çıkmamızı ve kalkülüs’teki kavramları kullanmamızı gerektirir. Leibniz kendi çalışmasını ortaya ilk attığında bu kavramlardan biri infinitesimal dediğimiz sonsuz küçük değerlerdi. Öyle bir ε>0 değer düşünün ki her r>0 reel sayısı için ε<r sağlanır. Herhangi bir pozitif reel sayısından küçük olan ama asla 0 olmayan sonsuz küçüklükte bir pozitif değerden bahsediyoruz. Bu bir sayı mıdır değil midir bu konu yazımızın kapsamı dışında kalacaktır. Ancak İngiliz ekolünden gelen ve bir teolog olan George Berkeley, böyle bir değerin bir sayı olamayacağına karşı çıkmıştır. Hatta bilimde infinitesimal değerlerin kullanılmasından o kadar rahatsızlık duymuştur ki 1734’te kaleme aldığı The Analyst kitabında bunu en ağır şekilde eleştirmiştir. (1) Berkeley, agnostiklerin (o dönemde bu kişilere free thinkers denmiştir) teolojiye saldırmasını anlamlandıramadığını, bu kişilerin bilimde infinitesimal değerleri kullanarak ne 0 olan ne de olmayan “hayalet” gibi değerleri kabul edişinin agnostiklerin kendi fikirleriyle çelişmesi olduğunu söylemiştir.
Dipnot:
(1) G. Berkeley, The Analyst The Analyst – a Discourse addressed to an Infidel Mathematician, 1734.
Yazar: Ahmet Çevik
Düşünbil Portal’da yayımlanan, Düşünbil yazar ve çevirmenlerine ait herhangi bir yazı, çeviri, makale ve haber izin alınmadan basılı olarak ya da internet ortamında kullanılamaz, çoğaltılamaz, yayınlanamaz. İzinsiz kullananlar hakkında hukuki yollara başvurulacaktır. Düşünbil Portal’da yayımlanan tüm özgün yazıların içeriğinden yazarları sorumludur.


