
Bu yazı “Matematik Tarihindeki Bazı Krizler” adlı daha genişçe bir yazının ikinci ve son bölümü olarak okuyucuya sunulmaktadır. Yazının ilk kısmını buradan okuyabilirsiniz.
Öklid dışı geometriler
Matematik tarihindeki bir diğer kriz geometriyle ilgilidir. Lise eğitimindeki geometri derslerinden bildiğimiz Öklid geometrisi’nin beş tane varsayımı (aksiyomu) vardır. Bu aksiyomlar şunlardır:
- Bir noktadan başka bir noktaya düz bir doğru çizilebilir.
- Bir doğru parçası, bir doğru olarak uzatılabilir.
- Herhangi bir merkeze ve yarıçapa sahip bir daire çizilebilir.
- Bütün dik açılar birbirlerine eşittir.
- (Paralellik Aksiyomu) Bir doğru iki doğruyu kesiyorsa, ve bu iki doğruyla aynı tarafta olan ve iç açılarının ölçüleri toplamı iki dik açının ölçüleri toplamından küçük iç açılar oluşturuyorsa, bu iki doğru o yönde sınırsız uzatıldığında mutlaka bir noktada kesişir.
Beşinci Aksiyom, aşağıdaki şekille daha iyi anlaşılabilir.
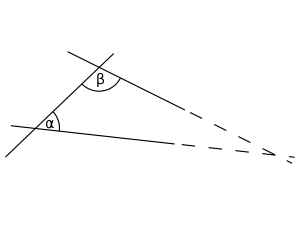
İki doğruyu kesen bir doğru alıyoruz. İç açıları α ve β olarak gösterelim. Eğer α + β < 180° ise, bu iki doğruyu uzattığımızda ikisi bir noktada kesişmek zorundadır.
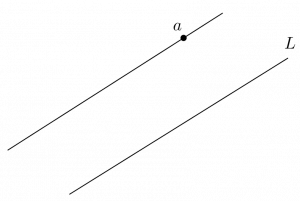
Beşinci aksiyoma aslında Paralellik Aksiyomu daha sonra denmiştir. 1846’da İskoç matematikçi John Playfair, bugün Playfair Aksiyomu olarak bilinen ve Öklid’in beşinci aksiyomu ile mantıksal olarak denk bir önerme göstermiştir: Bir L doğrusu alalım. Bu doğrunun dışında kalan herhangi bir a noktası alalım. O halde, a noktasından geçen ve L’ye paralel olan sadece tek bir doğru çizilebilir.
Paralellik Aksiyomu Öklid’den sonra ortaçağ matematikçileri tarafından diğer dört aksiyomdan kanıtlanmaya çalışılmışsa da başarılı olunamamıştır. Bu problem matematikçiler için çözümlenmesi gereken bir problem haline dönüşmüştür.
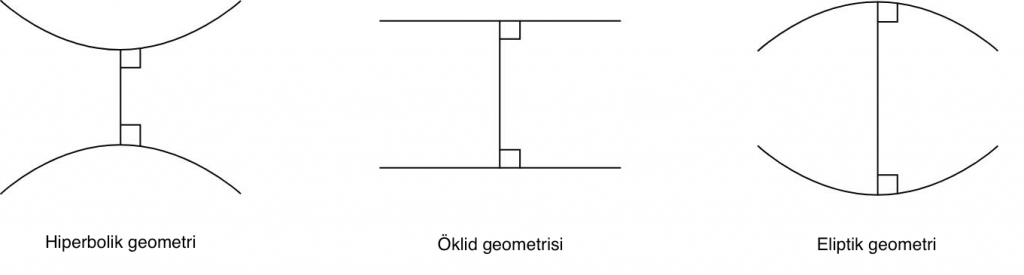
Öklid geometrisi tam anlamıyla bin yıllarca (2000 yıl) hüküm sürmüştür. 18’inci ve 19’uncu yüzyılda Parallellik Aksiyomu’nun doğru olmadığı geometriler bulunmuş, bu buluşlar matematiğe çok farklı bir heyecan getirmiştir. Carl Friedrich Gauss ve Nikolai İvanoviç Lobaçevski ve Janos Bolyai gibi matematikçiler Paralellik Aksiyomu’nu sağlamayan Öklid dışı geometrilerin var olduğunu göstermişlerdir. Bu geometriler, hiperbolik geometri ve Riemann geometrisi olarak da bilinen eliptik geometri‘dir.
Her ne kadar Öklid geometrisi çok sade, anlaşılır ve mükemmel gözükse de epey karmaşık ve gizemli olan fiziksel evrenin dilini anlatmaya yetmemiştir. Aslında Einstein’ın genel görecelik kuramına göre yer çekiminin uzayzamanı bükmesi, fiziksel uzayın Öklid geometrisiyle açıklanamayacağını işaret eder. Tek başına bu bilgi bile fiziksel uzayın Öklid dışı bir geometriye sahip olduğunu gösterir.
Öklid dışı geometrilerin varlığı 2000 yıllık bir geleneği değiştirmiş, hatta matematik felsefesinde çok önemli bir yere sahip olan Kant’ın Saf Aklın Eleştirisi’ndeki saf uzay formuyla ilgili varsayımların sorgulanabileceğini göstermiştir. Öklid dışı geometrilerin varlığının bir diğer etkisi, matematikteki önermelerin bazı ‘modellerde’ doğru, bazı ‘modellerde’ yanlış olabileceğini göstermiş olmasıdır. Paralellik Aksiyomu Öklid geometrisinde doğru kabul edilir, ancak bu aksiyom bahsi geçen Öklid dışı geometrilerde yanlıştır. Peki, mutlak bir geometri modeli var mıdır? Aslında bundan önce sormamız gereken soru şu: Matematikte mutlak bir geometri modeli almalı mıyız? Ya da, geometri dalının dışında, örneğin mutlak bir kümeler evreni almak zorunda mıyız? Farklı geometrilerin varlığı matematik felsefesinde çoğulcu (pluralist) bakış açısını güçlendiren bir sonuçtur. Tekçi (monist) bakış açısı, yani tek bir modelin ele alınması gerektiği görüşü, matematiksel önermelerin doğruluğunu ya da yanlışlığını sadece mevcut olan bu model içinde değerlendirmesi gerektiğini savunur.
Gödel’in Eksiklik Teoremi
Geometrideki krizden sonra 19’uncu yüzyılda Alman ekolünden gelen bazı matematikçiler mantıkla ve matematiğin temelleriyle ilgileniyorlardı. Bu matematikçiler arasından sembolik mantığın kurucularından Gottlob Frege ve sezgisel kümeler kuramını ortaya atan Georg Cantor’u en ön sıralarda gösterebiliriz. Öklid’e baktığımızda matematikte aksiyomatik yöntemin ön planda olduğunu görürüz. Rönesans ile beraber fizik ile matematiğin beraber yürüdüğünü gözlemleyebiliriz. Bu dönemlerde matematik tek başına soyut olarak değil, daha çok fiziksel olguları modellemek için ve fiziksel problemleri çözmek için kullanılmıştır. Ancak Cantor’la beraber bu yaklaşımın terk edildiğini ve sonrasında aksiyomatik yönteme tekrar geri dönüleceğinin sinyallerini görmeye başlıyoruz. Sezgisel kümeler kuramının Frege’nin mantık sistemiyle beraber kullanılması bir faciaya yol açar. Bertrand Russell, kümelerin gelişigüzel bir biçimde kullanılmasıyla ilgili Russell paradoksu olarak bilinen bir paradoks ortaya çıkarır ve matematikçiler bu sorunu çözmek için matematiğin temellerinin en baştan titizlikle ve dikkatlice kurulması gerektiğini düşünür.
Russell paradoksu berber paradoksuna dönüştürülebilir: “Bir kasabada öyle bir berber olsun ki bu berber sadece ve sadece kendi saçını kesmeyen insanların saçını kesmekte olsun. Herkes saçını ya kendi kesiyor ya da berbere kestiriyor. O halde berberin saçını kim keser?”
Cevap: Böyle bir berber olamaz.
Bu paradoks kümeler cinsinden de yazılabilir. Ancak bundan yazımızda bahsetmeyeceğiz.
Russell paradoksuyla beraber aslında 20’nci yüzyılda gerçekleşecek olan son krizin ilk sinyalleri verilmiştir. Alman matematikçi David Hilbert, matematiğin temelleriyle ilgili bu problemlerden kurtulmak için 20’nci yüzyılın başında çok büyük ve bir o kadar da iddialı bir proje başlatmıştır.
Bu projenin ne olduğunu açıklamak için önce aritmetikle ilgili önermelere bakalım. Örneğin “2+5<8” aritmetikte bir önermedir. Doğrudur da. Ancak biz doğruluğu ya da yanlışlığı ile ilgilenmeyelim şimdi. Daha karmaşık bir önerme de yazabiliriz. Örneğin “Her x sayısından daha büyük bir y sayısı vardır, öyle ki y sayısı 7’ye bölünebilirdir”. Bu da aritmetikle ilgili bir önermedir. Başka örnek olarak, “Her x sayısı için öyle bir y sayısı vardır ki x ile y aralarında asaldır” önermesini verebiliriz. Hatta “Her x asal sayısı için öyle bir y asal sayısı vardır ki x < y koşulu sağlanır” önermesi de aritmetikte bir önermedir. İşte aritmetikle ilgili herhangi bir önerme verildiğinde, bu önerme eğer doğruysa bize bunun kanıtını verecek bir bilgisayar programı düşünelim. Her şey çok kolay olur, matematikçinin matematik yapmasına gerek bile kalmazdı. 300 seneden fazla süredir kanıtlanamamış Fermat Teoremi sadece bir tıklamayla kanıtlanabilirdi. Matematik disiplini gerçekten bilgisayarlaştırılabilir mi? 20’nci yüzyılda matematik buna benzer şekilde biçimselleştirilmek istenmiştir. Bu, matematiği bilgisayarlaştırmak anlamına gelmeyebilir. O zamanlarda bilgisayar diye bir şey yoktu. Ancak proje başarıya ulaşsaydı sonuçlarından biri bu olurdu. Hilbert’in bu projesi Kurt Gödel’in 1931’deki Eksiklik Teoremi’yle başarısızlığa uğradı. Toplama ve çarpmayla ilgili aritmetiksel şeyleri kanıtlayabilen bir bilgisayar programı hiçbir zaman bütün aritmetiksel önermeleri kanıtlayamaz. Doğru olan ama bilgisayarın kanıtlayamadığı önermeler mutlaka olacaktır. Eksiklik Teoremi’nin yarattığı kriz başta Hilbert için çok büyük olmuştur. Aslında bu teoremin kriz yaratmasının sebebi, o dönemde bazı matematikçilerin ve mantıkçıların ideal bir matematiksel sistem elde etmek gibi bir ütopik fikre kapılmasıydı.
Gödel’in teoreminin birçok matematiksel ve felsefi sonuçları olmuştur. Ancak bu sonuçlardan şimdilik bahsedemeyeceğiz. Bu konuda daha fazla bilgi edinmek isteyen okurlara yakında çıkacak olan matematik felsefesi kitabımızı beklemesini söyleyerek yazımızı bitirelim.
Kaynaklar:
G. Berkeley, The Analyst The Analyst – a Discourse addressed to an Infidel Mathematician, 1734.
J. Playfair, Elements of Geometry, W. E. Dean, 1846.
A. Törün, Beşinci Aksiyom Krizi, Bilim ve Gelecek, Sayı 168, https://bilimvegelecek.com.tr/index.php/2018/02/01/besinci-aksiyom-krizi/
Yazar: Ahmet Çevik
Düşünbil Portal’da yayımlanan, Düşünbil yazar ve çevirmenlerine ait herhangi bir yazı, çeviri, makale ve haber izin alınmadan basılı olarak ya da internet ortamında kullanılamaz, çoğaltılamaz, yayınlanamaz. İzinsiz kullananlar hakkında hukuki yollara başvurulacaktır. Düşünbil Portal’da yayımlanan tüm özgün yazıların içeriğinden yazarları sorumludur.



